While ending our discussion on various approaches to partitioning, we saw how the typical hashing approaches fail when we encounter a node failure or when we have to add more nodes to our system. To review the reason for failure let us consider a system with 3 nodes where a client interacts with a particular node based on the value they get for each key from below function
hash(key) % number of nodes
So whatever value we get from the above function, we will store our key on the node assigned to that particular number. This will work perfectly fine and even satisfies our requirement for even distribution of key. But we do have one problem. What changes we need to do if we want to add another node to our system.
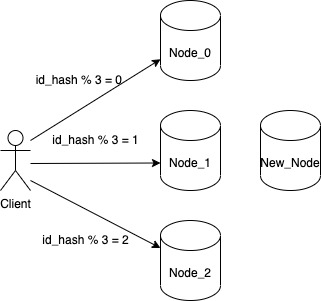
Our node allocation logic is no longer valid as it will not send any request to the new node. So in order to onboard the new node we will have to update the function to id_hash % 4. But doing just that doesn’t solves our problem because now client won’t be able to find the correct nodes to read the keys. Initially a key whose id_hash came out to be 10 was sent to Node_1 because id_hash(10) % 3 = 1. But now with updated function it will give a value of id_hash(10) % 4 = 2. When client will try to read from Node_2, it will get a KEY_NOT_FOUND error.
So in order to make our system work correctly, we will have to rerun our updated function for all the keys and move the keys to the correct node. This is lot of data movement due to rehashing when number of nodes changes and it will result in downtime for our application.
In case of addition or removal of a node, the best system will result in minimal movement of data. This helps in achieving a system where we have to do very less work to handle a failure or to onboard a new node. This is where consistent hashing comes into picture.
Before jumping into the details of how consistent hashing works, visualize all the nodes located on a circular ring covering a certain range of hash values. This is different in terms of how we typically visualize a system consisting of multiple nodes. In the below example we are assuming that our hash function will give us a value in range of 0 – 31. The range is decided based on the values a hash function you use and for simplicity we are considering a smaller range.
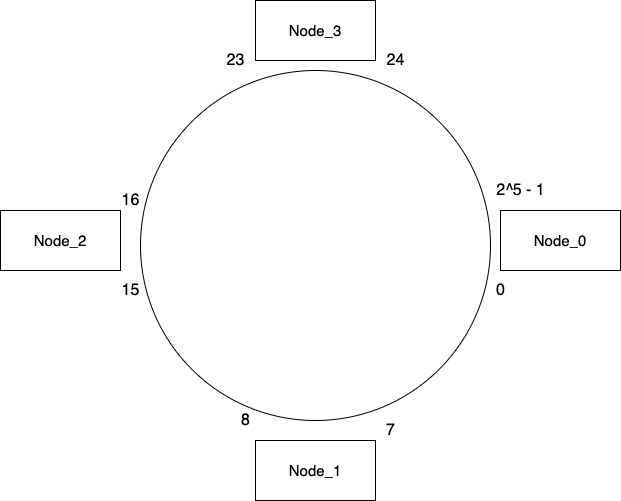
Now if our hash for a key results in a value of 6, we will figure out the piece of pie where our value can be located. In our example 6 will lie between Node_0 & Node_1. So we move in a clockwise direction and store the value in Node_1. The key will always be stored in the node that is the successor of hash value. So a hash value of 10 will be stored on Node_2, hash value of 20 will be stored on Node_3 and so on. The circle containing these nodes go around infinitely. So if hash results in a value of 30 then we will continue moving in clockwise order and store it on Node_0.
As part of consistent hashing we also store the same key in the next two nodes. So if we are storing a key on Node_0 then we also store it on Node_1 & Node_2 which are next in clockwise direction. This duplication of value on additional nodes is decided based on a configuration. So in the above case the value is 2 hence we duplicate the value on 2 additional nodes.
Now let us see how does the consistent hashing solves the problem we saw initially of adding a new node and removing a node in case of a failure.
Adding new node
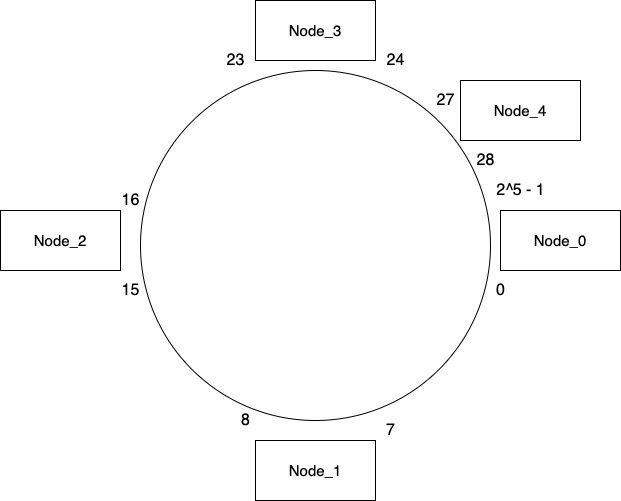
Consider we add a new node Node_4 between Node_3 & Node_0. We need to decide what keys we need to move in order to make our system ready for the client. Currently Node_0 consists of all the keys in range 24 – 31. Now when there is another node in between this range, Node_0 will be made responsible for only the keys in range 28 – 31. So we will need to move keys from range 24 – 27 on Node_3.
And that’s it. We don’t need to touch any of the other nodes and our system will work just fine as the key mapping for other nodes is still the same.
Only thing other nodes need to do is to update the node id where they are going to duplicate their keys. So after adding the new node, Node_3 now replicated its keys to Node_4 & Node_0 whereas previously it was copying it to Node_0 & Node_1. This can be done as part of a background job.
Handling node failure
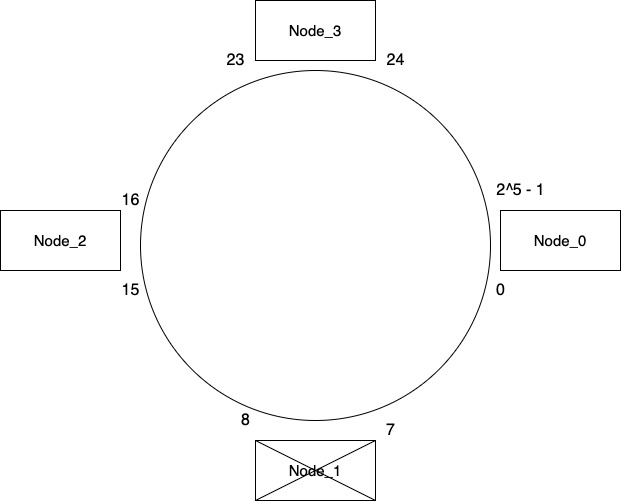
Consider what will happen when Node_1 fails. How do we distribute its keys which are in range 0-7 that it held among other nodes? Neighbor of Node_1 which is Node_2 takes over all the keys from Node_1. Now remember that as part of adding a key to any node, we duplicated that key to its neighboring nodes also. So if our system was functioning correctly before Node_1 failed then there is a high probability that Node_2 might already have all the keys from Node_1. We can run a background job to verify this and move any keys that we missed as part of duplication.
So even in case of a node failure our system works correctly without much data movement. Whenever we spin a new node to replace Node_1, it will be onboarded in the way we discussed above.
An edge case where consistent hashing might not work optimally is when a system has very few nodes. We might end up in an uneven distribution of keys across the nodes. One solution to this is to portray one node as multiple nodes. In other words Node_1 is represented as Node_1_1, Node_1_2 and so on to create an even distribution. So a system of say 3 nodes is portrayed as 9 nodes representing an even distribution of the circular ring. These are known as virtual nodes. One thing to ensure is that we want to distribute the virtual nodes randomly rather than sequentially in order to keep an even distribution.
Another advantage of having virtual nodes is better distribution of keys in case of a node failure. So instead of moving all the keys of the failed node onto another node, we move the keys from each of the virtual nodes to their neighbor. So if a node consisted of 100 keys and was represented as 10 virtual nodes then in case of failure we move 10 keys from each of the virtual nodes to their neighbor. This avoids overloading a node with a large chunk of data and keeps the distribution even across all nodes.
Consistent hashing is used by various data stores such as Riak. DynamoDb also uses consistent hashing with some additional improvements by leveraging virtual nodes.

Consistent hashing solves the problem that we saw happening with node failures in a typical partitioning system. We are able to achieve a well partitioned system with minimal data movement in terms of both onboarding a new node and node failure.

There is typo “from range 24 – 27 on Node_3” should be “from range 24 – 27 on Node_34”