Lamport Logical Clock: One after the another. But not together.

“Using a clock to model causality is like using a banana to model a nuclear reactor.”

– Leslie Lamport

As part of the last post, we looked into why is it difficult to measure time correctly in a distributed systems. In this post we will look into the Lamport logical clock that aims to find causality between two events. We will also see where it falls short and what other techniques can be used to solve for the remanning scenarios.

Let’s look at a system where a client is interacting with nodes to perform storage operations. For each request, the client’s request can land on any one of the nodes from the cluster. Now whenever a node performs a storage operation, it returns a monotonically increasing counter along with the response to the client. The node also persists the counter along with the value against the key in the storage. Client keeps track of this clock id and sends it next time when it is performing storage operations. This clock id is used to figure out the causality of events in a multi-node system. This approach is also known as versioned values.

Node updates its own clock id by using the clock id provided by client as following:

local_clock_id = MAX(local_clock_id + 1, request_clock_id)

A basic sequence diagram to demonstrate this interaction is shown below:

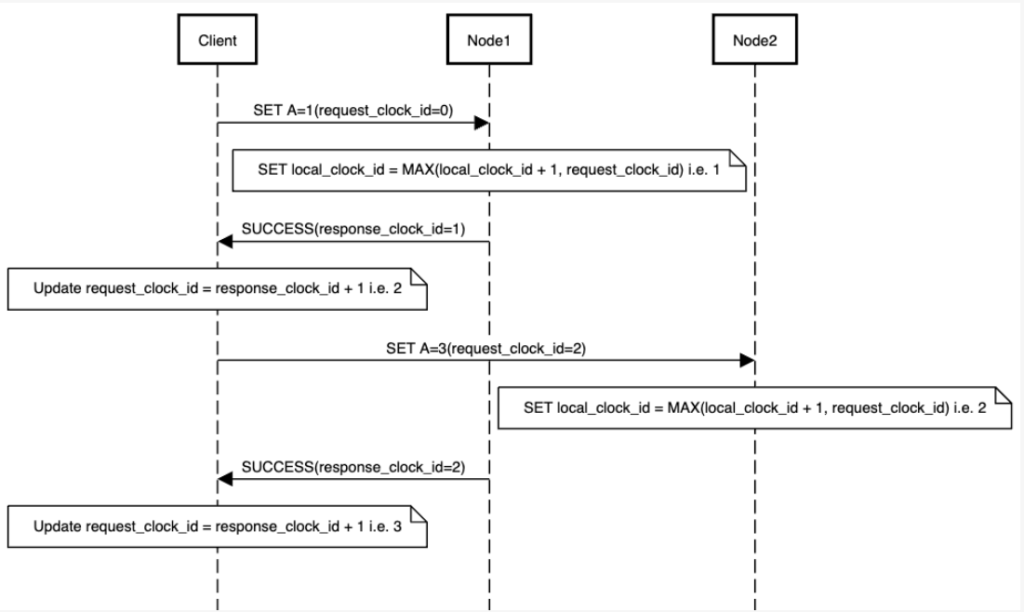
Now that we have different values for same resource across multiple nodes, we need to find a way to figure out what is the latest value of that resource. This is where versioning each value with a clock id comes in handy. A very basic approach is to send the reads to all the nodes and pick up the value associated with latest clock id.

So if there are two nodes in the cluster and we have to determine the latest value for a key, then we compare the clock id associated with the key from both nodes. The one with highest clock id is considered as the latest value. Though there can be a case where both nodes have the same clock id for the key and if so we will have to rely on some external mechanism to resolve the conflict.

The above approach might look simple but can end up being very compute intensive as you have to communicate among all the nodes in the cluster to determine the correct value. This can be improved by performing gossip based communication among nodes to sync their state with the cluster. It can be achieved using protocols such as SWIM. Now that nodes can sync with each other in the background and reach an eventually consistent state, we don’t have to communicate with all the nodes to determine the latest value.

But again we do need to realize that there is no silver bullet. Lamport clock also comes with its own set of limitations. Using lamport clock, we can confidently say that if event A occurred before event B then clock id of A will be less than clock id of B. But the inverse is not true so we cannot say that if clock id of A is less than clock id of B then event A happened before event B. This limitation makes the logical clock fall short when we need total ordering of events in scenarios such as a banking system where there is a concrete ordering of events is required. Also lamport clock cannot deterministically decide if two events occurred concurrently looking at their clock ids.

So we are doomed forever in search of correct time!

This is where the next concept of Vector clocks comes to rescue. In the next post we will look into how vector clocks helps us to overcome the limitations of Lamport clocks.Spoiler alert: Even vector clocks have limitations. Till then happy learning!